
This calculator computes volumes for some of the most common simple shapes. Alternatively, if the density of a substance is known, and is uniform, the volume can be calculated using its weight. Beyond this, shapes that cannot be described by known equations can be estimated using mathematical methods, such as the finite element method. The volumes of other even more complicated shapes can be calculated using integral calculus if a formula exists for the shape's boundary. In some cases, more complicated shapes can be broken down into simpler aggregate shapes, and the sum of their volumes is used to determine total volume. Volumes of many shapes can be calculated by using well-defined formulas. By convention, the volume of a container is typically its capacity, and how much fluid it is able to hold, rather than the amount of space that the actual container displaces. The SI unit for volume is the cubic meter, or m 3. Volume is the quantification of the three-dimensional space a substance occupies. Related Surface Area Calculator | Area Calculator Tube Volume Calculator Outer Diameter (d1) Square Pyramid Volume Calculator Base Edge (a) Base Radius (r)Ĭonical Frustum Volume Calculator Top Radius (r) Please provide any two values below to calculate. Rectangular Tank Volume Calculator Length (l)Ĭapsule Volume Calculator Base Radius (r) Sphere Volume Calculator Radius (r)Ĭylinder Volume Calculator Base Radius (r)
Please fill in the corresponding fields and click the "Calculate" button. The following is a list of volume calculators for several common shapes. We're really gonna take advantage of this.Home / math / volume calculator Volume Calculator So this relationship between circles and rotating vectors and sines and cosines is a very powerful idea. And you can see how sort of naturally they come out at different phases, right. So I like to visualize thisīecause this rotating vector is a really simple and powerful idea, and we can see how it actually generates, it's a way to generate It was the projection on the y-axis, produced the
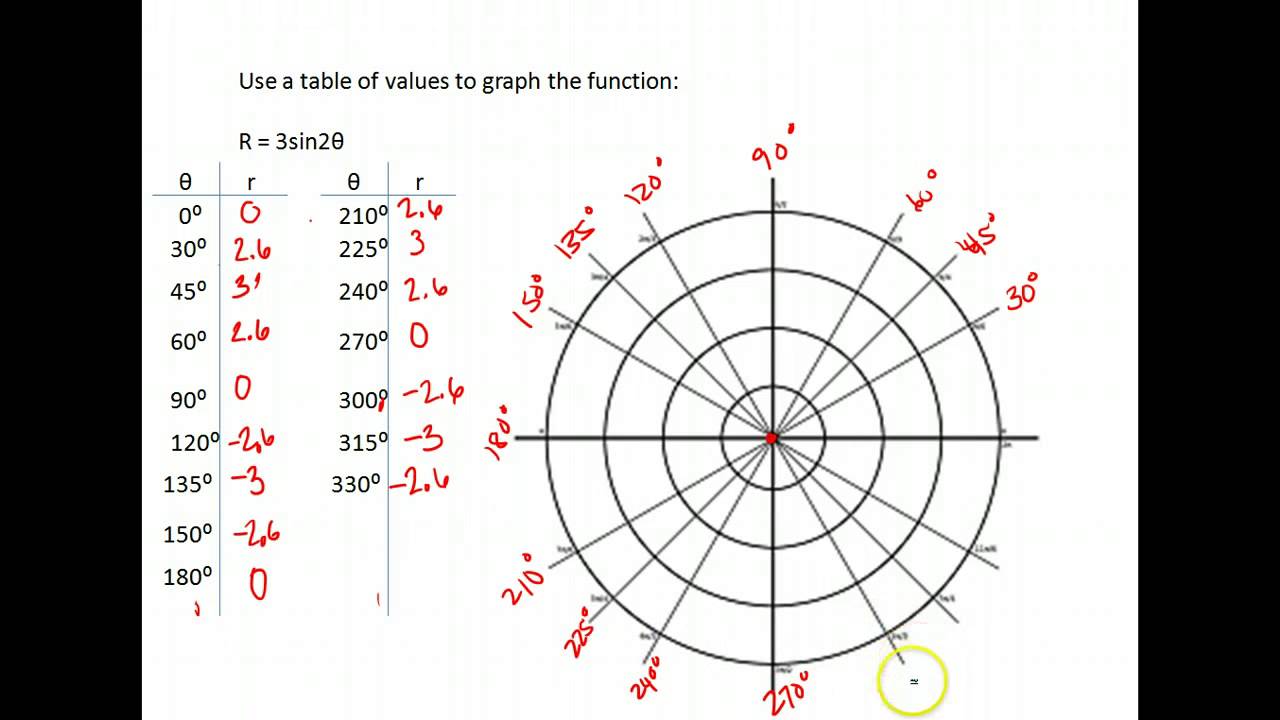
The cosine comes out the bottom because it's the projection on the x-axis, and when we did the sine, Visualize the cosine curve getting generated by a vector And when we get back to zero again, the projection is to this point here. Will be at the same point as before, as the one above, but it'll be on this part of the curve here. We're moving this radius vector around in a circle like this. When the arrow is straight up, we are at this point right here, we go back to the axis. We go to a higher angle, this projection now moves If I project that down onto the angle zero, that's this point right here on the curve. So in this diagram, the cosine of theta is actually the x value So cosine of theta equals adjacent which is x, the x value, divided by hypotenuse which is one. And our definition of cosine was adjacent over hypotenuse. We project the projection of this value onto this time Thing with the cosine function that we did with sine, where So every two pi, if I go off the screen, every two pi comes backĪnd repeats to zero. Now when the angle getsīack all the way to zero, of course, the sine functionĬomes all the way back to zero and then it repeats againĪs our vector swings around the other way. Way, down here like this, right, you can see that, that plots over there like that. And then as theta swingsĪround the circle, I'm gonna plot the different values of y. So, if I plot this on a curve, this is an angle and Iīasically go over here and plot it like that. The hypotenuse is one in all cases around this. So sine of theta is actually equal to y over the hypotenuse and So this is the opposite side and that distance is the opposite leg of that triangle, is The definition of sine of theta, this will be theta here, is opposite over hypotenuse. So if I draw this line up here, it's on a unit circle, So if we draw a line on here, let's make this circle a radius one. Out on a straight line instead of wrapped around this circle. Is the theta axis in this plot, where theta has been plotted This is a plot of the sine function where the angle, theta, this Clear off the screen here and we're gonna talk about the


 0 kommentar(er)
0 kommentar(er)
